Algo sobre conjuntos (Problema 5)

Creo que puedo hablar por todos cuando digo que hemos trabajado con diagramas de Venn al aprender matemática. Probablemente en la primaria. Al menos yo recuerdo que hacíamos en la mesa unos círculos con lana y le poníamos adentro objetos que eran los elementos del conjunto. Esa imagen la tengo grabada en la cabeza.

Resulta que los diagramas de Venn plantean algunos problemas no relacionados con la teoría de conjuntos, pero si con teoría de grafos y cosas relacionadas.

Para empezar digamos que un conjunto de líneas cerradas (por ejemplo círculo, cuadrado, elipse, etc) será llamado diagrama de Venn cuando cumpla una única condición:

Cada zona determinada por las líneas debe estar encerrada por un único conjunto de líneas. O sea, si tenemos dos círculos, a los que llamamos A y B, que se intersecan en dos puntos, quedan determinadas 3 zonas, una de ellas sólo está encerrada por A, otra por B y otra por AyB.
Entonces esa disposión es un diagrama de Venn.

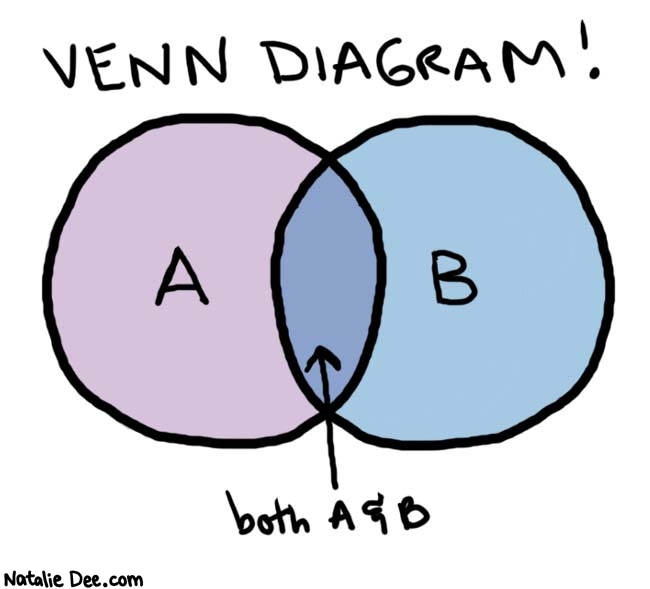Imagen tomada de http://www.nataliedee.com

Aquí tenemos una imagen que ilustra perfectamente lo dicho. Está en inglés porque la saqué de otra página (o alguien creía que me iba a poner a producir material original para esto... no por ahora al menos).
Si juntamos tres círculos, podemos lograr el mismo objetivo, con una zona en el medio que pertenece a los tres conjuntos, tres zonas que pertenecen a dos de ellos cada una, y otras tres que pertenecen a uno solo de ellos cada una.
Les pongo una imagen, que dice más que mil palabras (o al menos más que las 43 que usé en el párrafo anterior para explicarlo).

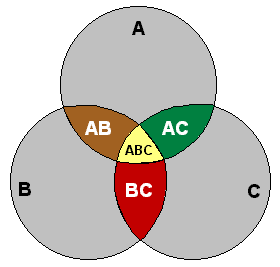Imagen tomada de http://www.yourdictionary.com

Y hasta ahí se llega con círculos. Con cuatro ya no se puede disponer de ellos en posición alguna que provea zonas para cada combinación de conjuntos, es decir, para poder hacer cuatro conjuntos y representarlo en un diagrama de Venn, habría que deformar un poco las figuras, como se ve en esta imagen:

Imagen tomada de http://www.graphic.org

Se puede demostrar que 3 es el máximo DV que se puede hacer con círculos, así como se puede demostrar que si se lo hace con elipses, el máximo es 5. También existe la posibilidad de hacerlo con triángulos, por ejemplo:

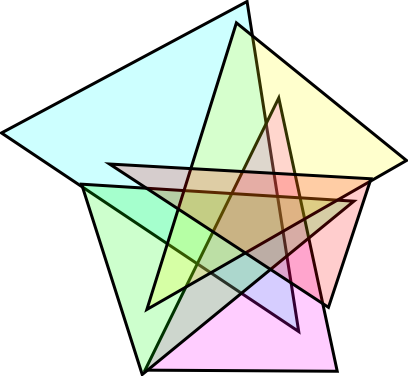Imagen tomada dehttp://www.fejes.ca

              Tenemos 5 triángulos que determinan una cierta cantidad de zonas que cumplen lo antedicho, por lo que se trata de un diagrama de Venn de 5 conjuntos, logrado con 5 triángulos.
Lo que me interesa es encontrar un diagrama de Venn formado por 6 triángulos... el problema es que no se sabe si existe... es decir, es un problema abierto.
Si alguien quiere, se pone a verlo y pensarlo. Puede llegar a conseguir fama (pequeña y sólo entre matemáticos, pero fama al fin).


Los dejo con la inquietud.


Para que no se frustren, les doy otra cosa para resolver: hallar una fórmula para determinar la cantidad de zonas determinadas por n conjuntos.

Saludos....

RESPUESTA ACÁ